Ankit Mahajan    Projects    Misc    Google scholar

Projects

My research in the Sharma group has broadly focused on developing accurate and efficient wave function based methods to study strongly correlated electronic systems. Examples of such systems include metalloenzymes with transition metal centers, molecular magnets, and transition metal oxides. Cheaper mean-field methods or density functional theory tend to perform poorly for these systems. Wave function based methods, while accurate, suffer from the “curse of dimensionality” arising from the exponential increase in the dimension of the Hilbert space for larger systems. Monte Carlo techniques are perfectly suited for such high dimensional problems. While, traditionally, real space quantum Monte Carlo methods, working in the continuum, have been used to study ab initio systems, methods set in the discrete orbital space have received a lot of attention lately for various reasons. In the past few years, I have been studying these methods resulting from the marriage of conventional wave function quantum chemistry with quantum Monte Carlo. I have also spent some time implementing some of these methods in an efficient C++ code available here.

  • Novel wave functions in QMC

    One attractive feature of orbital space QMC methods is that they afford more flexibility in the choice of wave functions used to control the sign problem. In particular, Jastrow wave functions have been shown to capture strong correlations in a compact ansatz that can be evaluated in polynomial time with QMC. While traditional quantum chemistry methods have employed particle-hole excitations to capture electron correlation, this framework is not well suited for describing strongly interacting and, as a result, often localized electrons. The GIFs below illustrate this point. They were made by sampling the electronic configurations in the ground state of the six site Hubbard model. The more a configuration contributes to the ground state, the more it gets sampled. The local and canonical pictures show the same state but in different bases. As can be seen, while particle-hole excitations in a canonical basis can describe correlations for arising from weak interactions with few low-rank excitations, they cannot describe strong interactions efficiently. In the local basis, Jastrow wave functions represent the wave function by putting a penalty on the particle number fluctuations, which are rare when interactions are strong.

    weak interactions strong interactions
    locu1 locu10
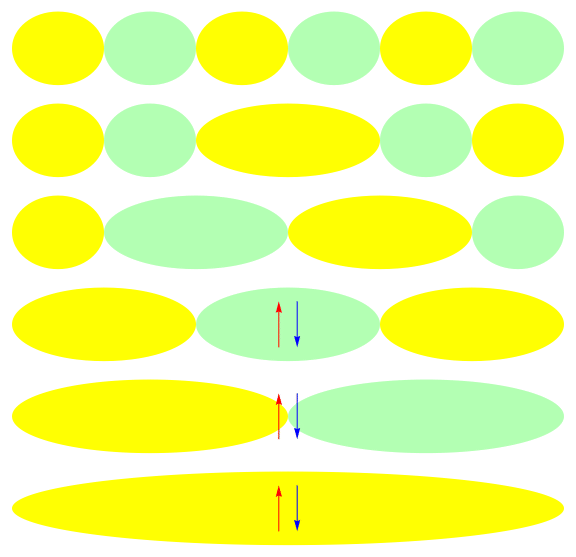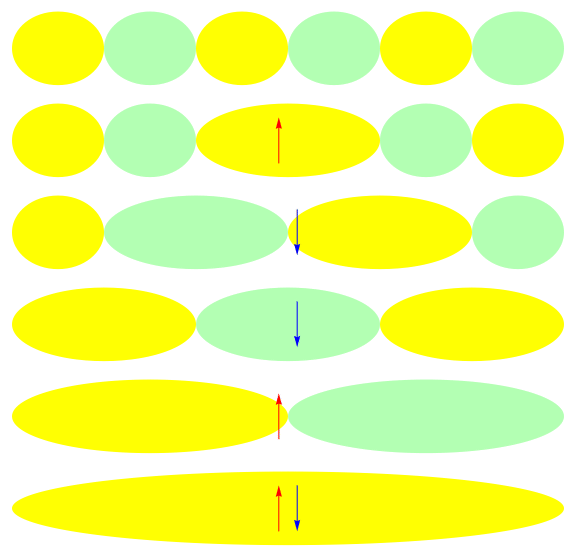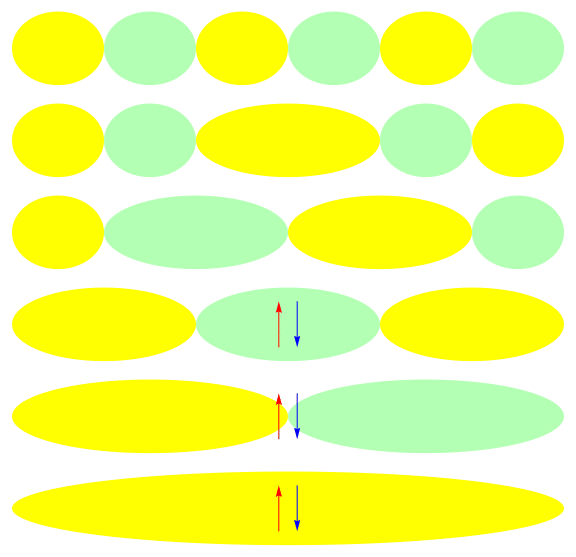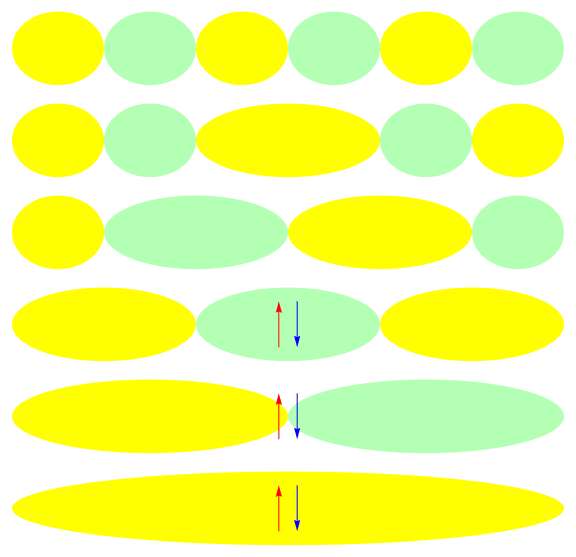
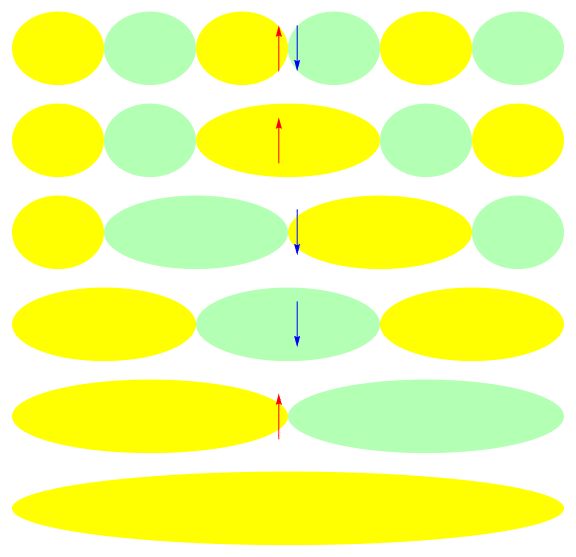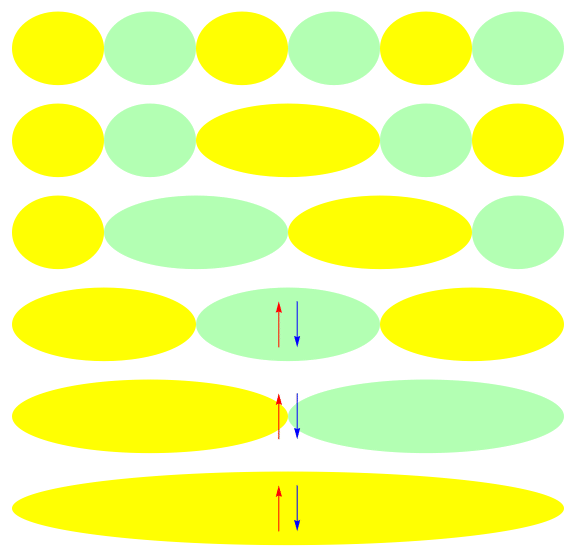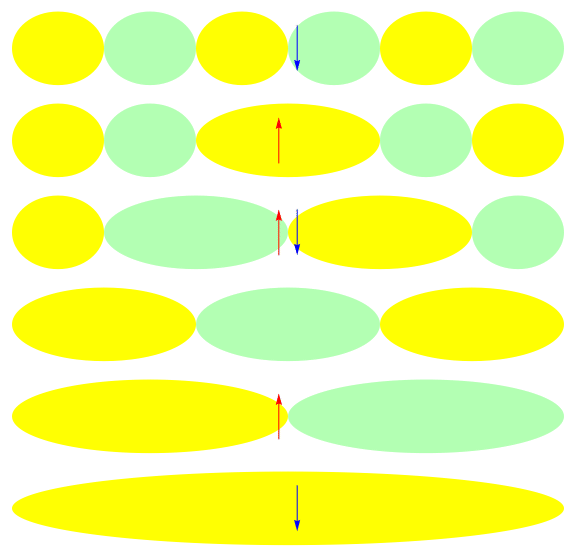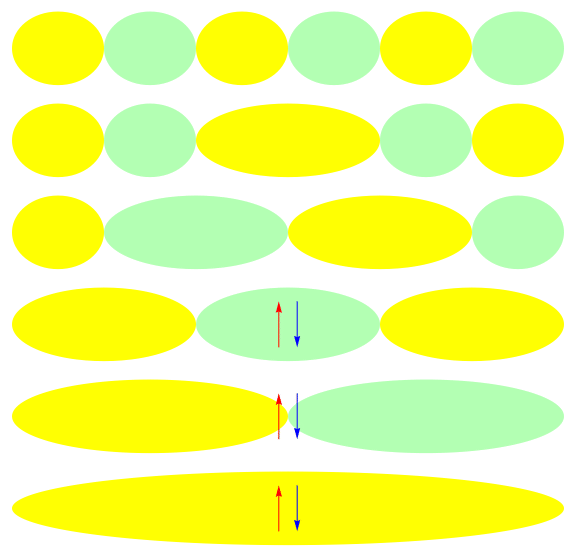
    canu1 canu10

    The Jastrow factor itself is completely bosonic. For describing electrons, it is used as a correlator on top of a fermionic reference wave function. Also, while the Jastrow factor is good at representing Coulombic interactions, it does not effectively capture more general interactions, like spin and charge exchange. Thus an accurate reference wave function is required when such interactions are present in the system under study. We have studied two possible reference wave functions:

    • Symmetry projected mean-field states[1, 2]: These states generalize the simplest known mean-field state, the Slater determinant, by explicitly breaking and subsequently projecting symmetries of the Hamiltonian. Projection of symmetries like complex conjugation, spin, and number can be performed trivially in QMC, at essentially mean-field cost.

    • Multi-Slater states[3]: These are conventional particle-hole excitation states known as configuration interaction in chemistry and RPA in physics. The Jastrow factor encodes the strong interactions, and the rest of the interactions can be accounted for efficiently with multi-Slater reference. QMC calculations of multi-Slater states can be very expensive when a large number of configurations are used. We formulated an efficient algorithm to lower this cost scaling substantially by using patterns arising in the matrix elements of long strings of creation and annihilation operators in the energy expression. This development has allowed us to use a much larger number of configurations than possible with existing methods. We hope to use this algorithm in different methods like auxiliary field QMC and Green’s function QMC.

[1] Mahajan, A. and Sharma, S., 2019. Symmetry-projected Jastrow mean-field wave function in variational Monte Carlo. The Journal of Physical Chemistry A, 123(17), arxiv:1902.07690.

[2] Sabzevari, I., Mahajan, A. and Sharma, S., 2020. An accelerated linear method for optimizing non-linear wavefunctions in variational Monte Carlo. The Journal of Chemical Physics, 152(2), arXiv:1908.04423.

[3] Mahajan, A. and Sharma, S., 2020. Efficient local energy evaluation for multi-Slater wave functions in orbital space quantum Monte Carlo. The Journal of Chemical Physics, accepted, arXiv: 2008.06477.

  • Stochastic multireference configuration interaction and perturbation theory

    Strongly interacting electronic systems often have a few strongly interacting degrees of freedom and a much larger number of weakly interacting ones, arising from high energy excitations. Accounting for these high energy excitations, termed dynamic correlation, is often important to obtain quantitatively accurate answers comparable to experiments. Sometimes they even change the electronic structure qualitatively. Deterministic methods used to calculate dynamic correlations have very steep scaling with system size because they require high-order reduced density matrices (aka correlation functions). We showed that performing the energy calculations stochastically allows one to avoid explicitly calculating these large tensors and results in a much lower scaling method [4]. We have used this method in interesting model metalloenzyme systems, like iron porphyrin and dicopper complexes, to calculate their electronic structure with high accuracy [5].

[4] Mahajan, A., Blunt, N.S., Sabzevari, I. and Sharma, S., 2019. Multireference configuration interaction and perturbation theory without reduced density matrices. The Journal of Chemical Physics, 151(21), arXiv:1909.06935 (Featured article).

[5] Blunt, N.S., Mahajan, A. and Sharma, S., 2020. Efficient multireference perturbation theory without high-order reduced density matrices. The Journal of Chemical Physics, 153(16), arXiv: 2008.00220.